導入

先日、直線の線形回帰を行う記事を書きました。
今回は、前の記事で行った線形回帰の基底を変更することで、非線形な回帰を行います。 hotaru-conny.hatenablog.com

線形回帰と多項式回帰

前回行った線形回帰は、 $x$ と $y$ の学習データをもとに、以下の式の $a_1$ と $a_0$ を求める回帰でした。

$\displaystyle y = a_1 x + a_0\tag{1}$

前回の線形回帰では、 $x$ と $y$ の関係を直線の式で仮定して、そのパラメータを求めたわけです。
となれば、直線以外の式を仮定して回帰を行うことも可能です。シンプルな例でいえば、以下の式で多項式を仮定すると多項式回帰を行うことができます。

$\displaystyle y = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0\tag{2}$

この多項式回帰では、nが2以上であれば、直線的でない非線形な回帰を行うことができます。

scikit-learnのLinearRegression()

scikit-learnにおけるLinearRegression()は、関数名こそ線形回帰っぽい名前ですが、直線の回帰だけでなく、基底に対する重み付き和に対する回帰として使えます。

前回行った回帰は、1入力1出力で、以下の式のパラメータを求めるものでした。

$\displaystyle y = a_1 x + a_0\tag{1}$

これに対し、多入力1出力の線形回帰は、以下のような式になります。

$\displaystyle y = a_n x_n + a_{n-1} x_{n-1} + \cdots+ a_1 x_1 + a_0\tag{3}$

scikit-learnのLinearRegression()は、以下のように機能するわけです。

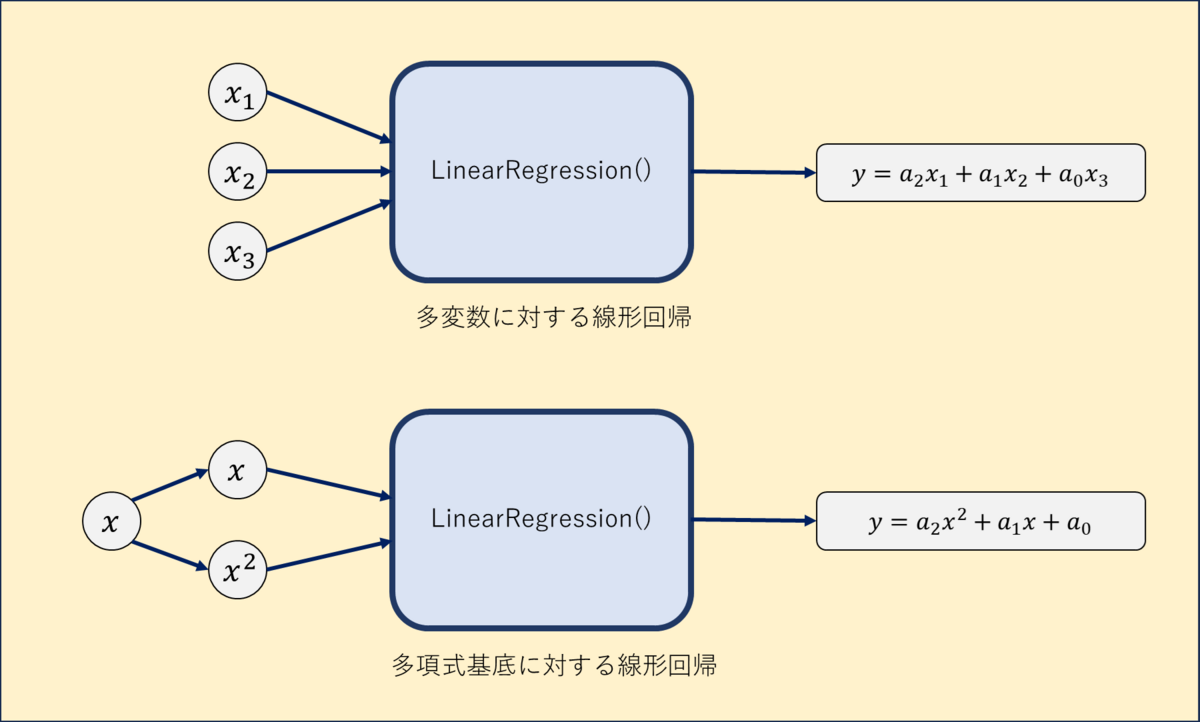
ここで、多変数に対する線形回帰

$\displaystyle y = a_n x_n + a_{n-1} x_{n-1} + \cdots+ a_1 x_1 + a_0\tag{3}$

と、多項式回帰

$\displaystyle y = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0\tag{2}$

は、式の形が似ていますよね。実際、式(3)の $x_i$ を $x^{i}$ に置き換えることで、式(2)を得ることができます。したがって、scikit-learnの上では、 ${x^{n}, x^{n-1}, \cdots, x, 1}$ を基底としてLinearRegression()を使用することで、多項式回帰を行うことができます。

具体例を図で示しておきましょう。 $x_1, x_2$ の2つの入力から $y$ を推論する線形回帰と同様に、1つの入力 $x$ をもとに、 $x^{2}, x$ を仮想的に2つの入力とみなして線形回帰を行うことで、2次元の多項式回帰を実現します。

多項式回帰の実践

実際に多項式回帰を行っていきます。
今回は、事前に作った多項式に確率的な誤差を乗せたデータを作成して、そのデータに対して回帰を行います。

#scikit-learnで多項式回帰
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt
import numpy as np

#データ数
num_points = 100
#係数
a2 = 3.5
a1 = 2.5
a0 = 1.0
#誤差の平均と標準偏差
mean = 0
std = 20
#データを作成
x = np.random.uniform(-10, 10, num_points)
y = a2 * x ** 2 + a1 * x + a0 + np.random.normal(mean, std, num_points)

x = x.reshape(-1, 1)
y = y.reshape(-1, 1)

#線形回帰モデルを使う
model = LinearRegression()

#2次元の多項式基底を作成
quadratic = PolynomialFeatures(degree=2)

#xに多項式特徴量を適用
x_poly = quadratic.fit_transform(x)

#モデルにフィッティング
model.fit(x_poly, y)

#プロット用のデータを生成して予測
x_plot = np.linspace(-10, 10, 100).reshape(-1, 1)
x_plot_poly = quadratic.transform(x_plot)
y_plot = model.predict(x_plot_poly)
#データをプロット
plt.scatter(x, y)

#回帰直線をプロット
plt.plot(x_plot, y_plot, color="red")

実行結果は以下になります。

fit_transform()とtransform()

ここで、学習時のxのデータの処理には、quadratic.fit_transform(x)を使っているのに対し、推論時のデータの処理には、quadratic.transform(x)を使っています。
fit_transform()は、引数のデータについて、最大値や平均といった統計データを計算して、どのような前処理を行うか決定し、変換を行う関数です。この時決定された前処理の内容は、メモリに保存されています。
transform()は、メモリに保存されている前処理内容を、単に適用する関数です。
すなわち、学習用データに対しては、前処理の方法を決定&変換しているのに対し、テスト用データに対しては、学習用データに対して行ったのと同じ変換を行っています。

多項式以外の非線形回帰

式(2)の基底を $x^{n}, x^{n-1}, \cdots, x, 1$ に変更することで、多項式回帰を行うことができました。なら、基底をさらに別のもの、例えば $e^{x}, x, 1$ なんかにしても回帰ができると考えられますね。試しにやってみましょう。

import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

#データセット生成
#データ数
num_points = 100
#係数
a2 = 3.5
a1 = -3000
a0 = 1.0
#誤差の平均と標準偏差
mean = 0
std = 5000
x = np.linspace(0, 10, num_points)
y = a2 * np.exp(x) + a1 * x + a0 + np.random.normal(mean, std, num_points)
x = x.reshape(-1, 1)
y = y.reshape(-1, 1)

#基底を自分で設定
base = np.hstack([np.exp(x), x, np.ones_like(x)])

#モデルの学習
model = LinearRegression()
model.fit(base, y)

#予測
y_pred = model.predict(base)

#プロット
plt.scatter(x, y)
plt.plot(x, y_pred, color='red')
plt.show()

実行結果は以下になります。

対象データは、 $y=3.5e^{x}-3000x+1$ です。 $x$ が小さい部分では $-3000x$ の項が支配的で右下がりに、 $x$ が大きい部分では $3.5e^{x}$ 成分が支配的になって右肩上がりになっています。また、回帰の結果でもこのデータを適切に推論できていることが確認できますね。